Skip to main content

Section 6.5 Inverse Trig Functions

Does \(f(x)=\sin(x)\) have an inverse function?

No, it is not one-to-one. However, if we restrict the domain to \(\left[ -\dfrac{\pi}{2} \mbox{ , } \dfrac{\pi}{2} \right]\text{,}\) then it is a one-to-one function. This is called the "restricted" sine function, and the inverse gives \(\arcsin(x) \mbox{ or } \sin^{-1}(x)\text{.}\)

Figure 6.5.1. restricted sin(x)
Figure 6.5.2. arcsin(x)

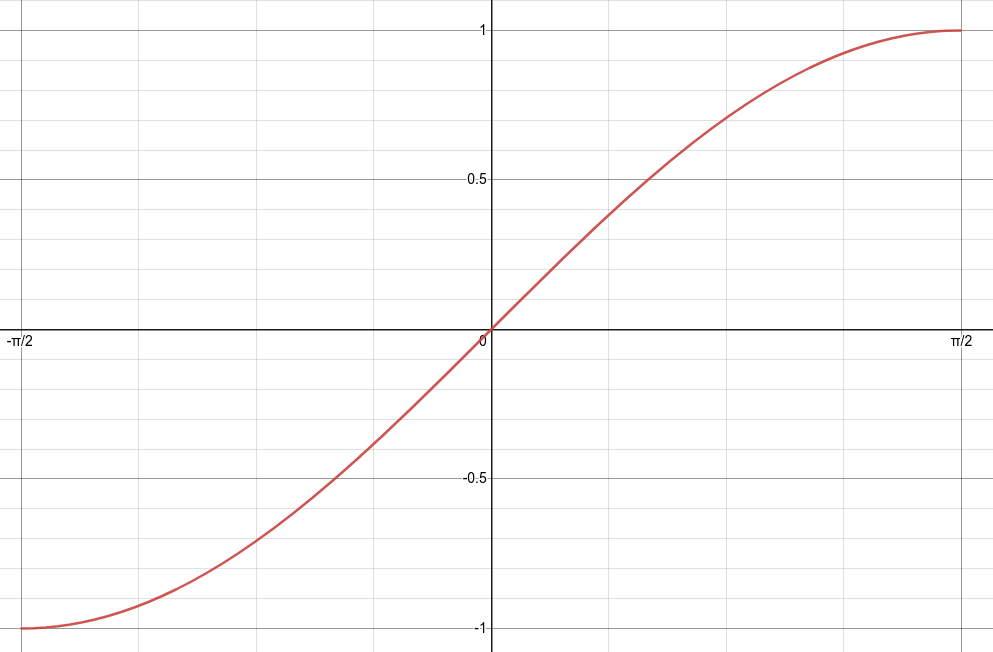
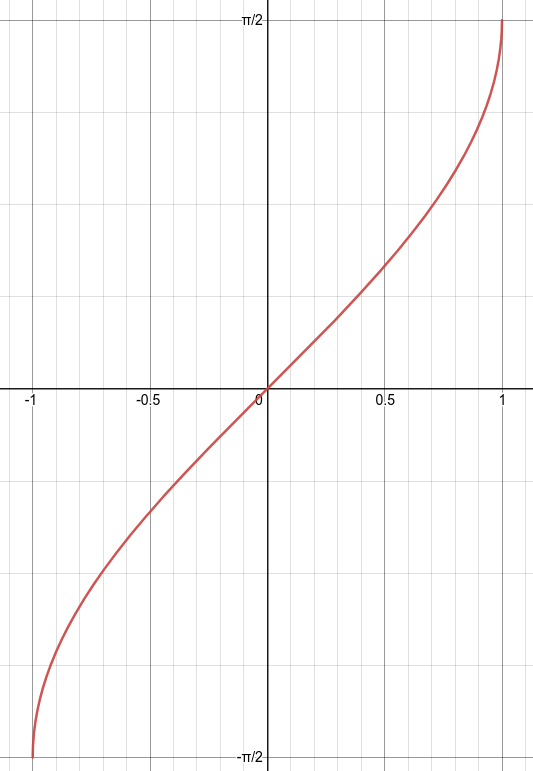
A similar thing is true for cosine. Inverse of restricted cosine with a domain of \(\left[ 0 \mbox{ , } \pi \right]\text{,}\) gives us \(\arccos(x) \mbox{ or } \cos^{-1}(x)\text{.}\)

Figure 6.5.3. cos(x)
Figure 6.5.4. arccos(x)

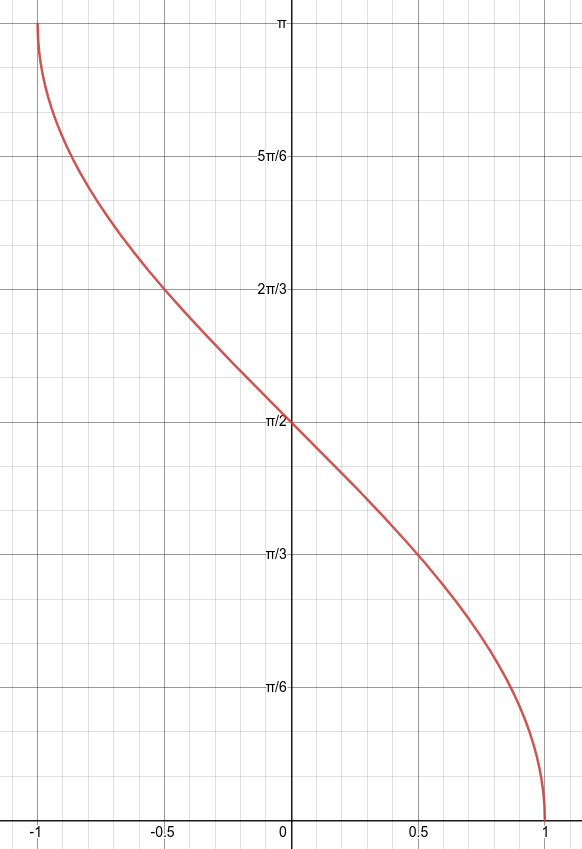
Tangent on the other hand repeats and can be restricted to \(\left( -\dfrac{\pi}{2} \mbox{ , } \dfrac{\pi}{2} \right)\) where it has two vertical asymptotes. When inversed, there are then two horizontal asymptotes from \(\left[ -\infty \mbox{ , } \infty \right]\text{.}\)

Figure 6.5.5. tan(x)
Figure 6.5.6. arctan(x)

Subsection 6.5.1 Triangle Method

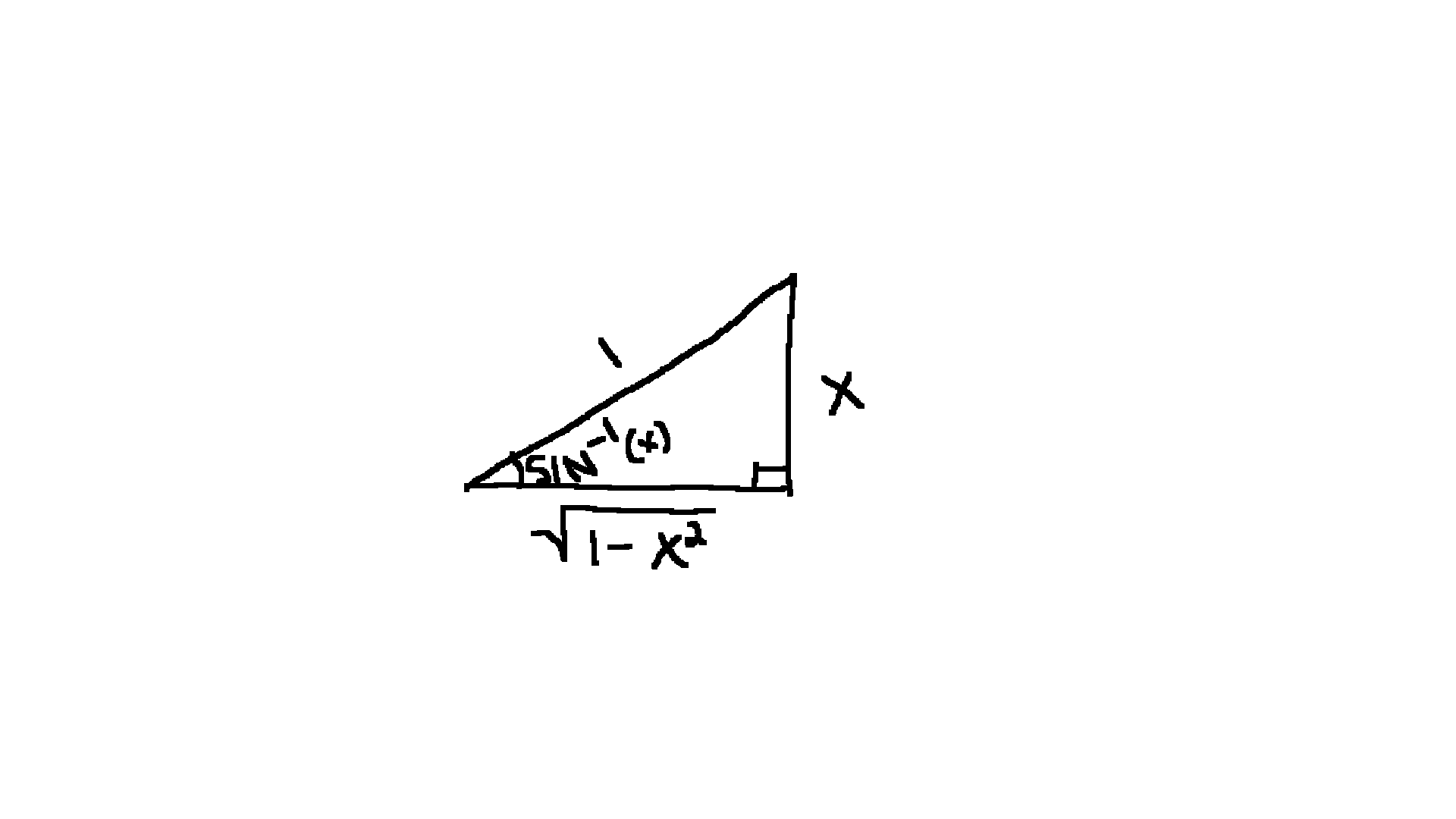
What is \(\sin(\tan^{-1}(x))\text{?}\)

Recall that tangent is opposite of adjacent, so we can represent this as \(\dfrac{x}{1}\text{,}\) plug it in, and then solve for the hypotenuse. This leaves us with the image below.

Figure 6.5.7.
Now, let's take the sine of this function. That would be opposite over hypotenuse or \(\dfrac{x}{\sqrt{(1+x^2)}}\text{.}\) That is our final answer.

Subsection 6.5.2 Derivatives

How would we find the derivative of \(y = \sin^{-1}(x)\text{?}\)

Note 6.5.8.

If \(y = \sin^{-1}(x)\text{,}\) then \(\sin(y) = \sin(\sin^{-1}(x))\) and \(\sin(y) = x\text{.}\)

\begin{equation*} \sin(y) = x \end{equation*}

Now, take the derivative of both sides with respect to x.

\begin{align*} \cos(y) \cdot \dfrac{dy}{dx} \amp = 1 \\ \dfrac{dy}{dx} \amp = \dfrac{1}{\cos(y)} \\ \amp = \dfrac{1}{\cos(\sin^{-1}(x))} \\ \amp = \dfrac{1}{\sqrt{1-x^2}} \end{align*}

Figure 6.5.9.

If we repeat this process for the other trig functions we get the following list:

  • \(\displaystyle \dfrac{dy}{dx}(\sin^{-1}(x) = \dfrac{1}{\sqrt{1-x^2}} \)

  • \(\displaystyle \dfrac{dy}{dx}(\cos^{-1}(x) = - \dfrac{1}{\sqrt{1-x^2}} \)

  • \(\displaystyle \dfrac{dy}{dx}(\tan^{-1}(x) = \dfrac{1}{1+x^2} \)

Subsection 6.5.3 Integrals

Idefinite intregrals are just the opposite of derivatives, so we can simply reverse the opperations and add c.

  • \(\displaystyle \int \dfrac{1}{\sqrt{1-x^2}} dx = \sin^{-1}(x) + c \)

  • \(\displaystyle - \int \dfrac{1}{\sqrt{1-x^2}} dx = \cos^{-1}(x) + c \)

  • \(\displaystyle \int \dfrac{1}{1+x^2} dx = \tan^{-1}(x) + c \)