Calculus Notes

Theorem 1.2.1.

1. \(\displaystyle\lim_{x \to a} k = k\)

   

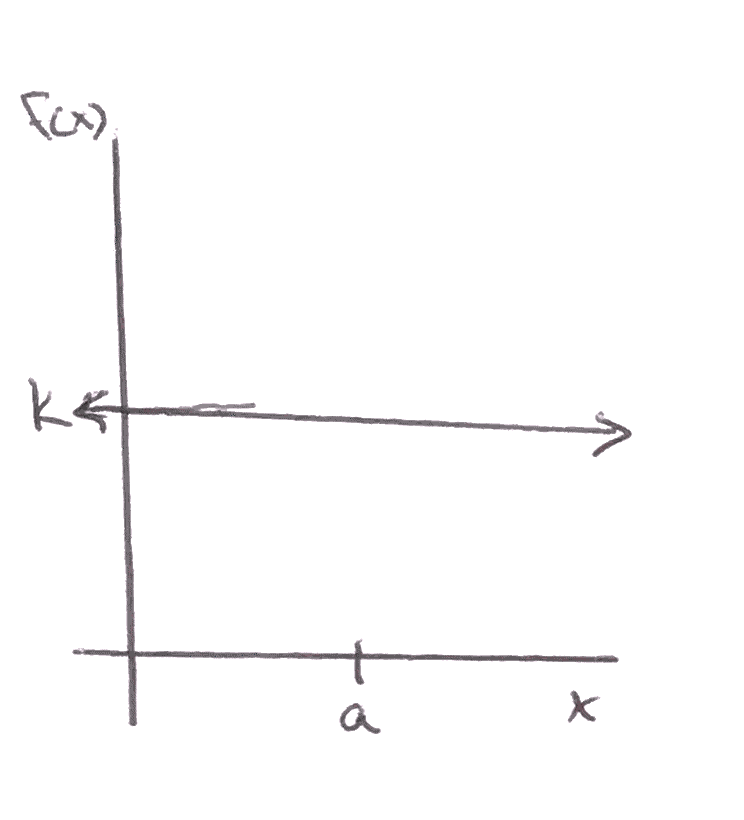
   the limit of a constant function is that constant value as \(x\) approaches any number

2. \(\displaystyle\lim_{x \to a} x = a\)

   

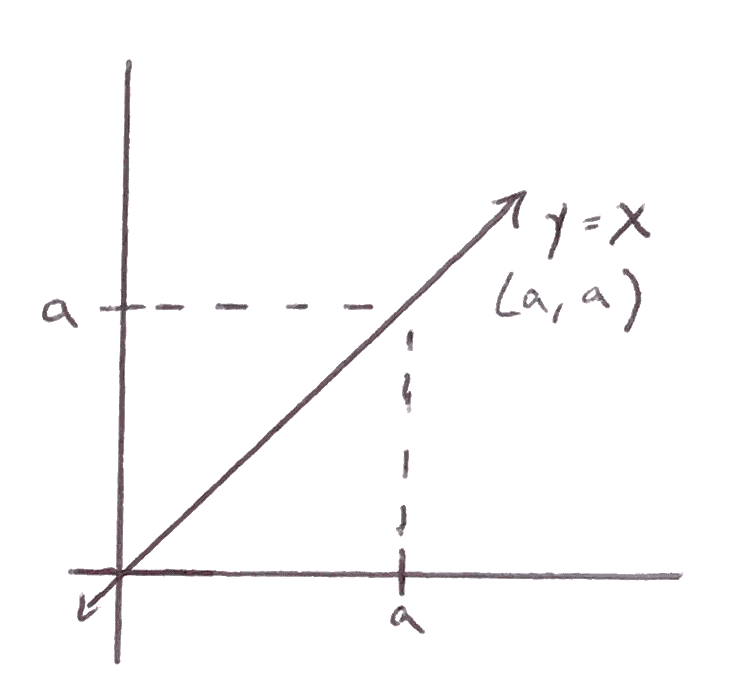
   the limit of a function at a y-value of \(a\) is \(a\) as x approaches \(a\)

Theorem 1.2.4.

Let \(a\text{,}\) \(L_{1}\text{,}\) and \(L_{2}\) be real numbers.

1. \(\displaystyle\lim_{x \to a} \left( f(x) + g(x) \right) = \left( \displaystyle\lim_{x \to a} f(x) \right) + \left( \displaystyle\lim_{x \to a} g(x) \right) = L_{1} + L_{2} \)

   Note 1.2.5.

   The limit of of the sum is the sum of the limits.

2. The above is true also for the difference.

3. \(\displaystyle \displaystyle\lim_{x \to a} \left( f(x) \cdot g(x) \right) = \left( \displaystyle\lim_{x \to a} f(x) \right) \cdot \left( \displaystyle\lim_{x \to a} g(x) \right)\)

4. \(\displaystyle\lim_{x \to a} \left( f(x) / g(x) \right) = \left( \displaystyle\lim_{x \to a} f(x) \right) / \left( \displaystyle\lim_{x \to a} g(x) \right)\)

   Note 1.2.6.

   This is true provided that \(\displaystyle\lim_{x \to a} f(x) \neq 0\text{.}\)

5. \(\displaystyle\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\displaystyle\lim_{x \to a} f(x)}\)

   Note 1.2.7.

   This is true provided that \(\displaystyle\lim_{x \to a} f(x) > 0\) if \(n\) is even.

Theorem 1.2.8.

Let any polynomial \(p(x) = C_{0} + C_{1}x^{1} + \dots + C_{n}x^{n}\) and any real number \(a\text{,}\)

Theorem 1.2.9.

Let \(f(x) = \dfrac{p(x)}{q(x)}\) be a rational function (\(p(x)\) and \(q(x)\) are both polynomials),

1. if \(q(a) \neq 0\text{,}\) then \(\displaystyle\lim_{x \to a} f(x) = f(a)\)

2. if \(q(a) = 0\text{,}\) then the limit is technically DNE

For limit of the form \(f(x) = \dfrac{p(x)}{q(x)}\) as \(x \to a\)

1. if there are no zeros, just plug in

2. if there is a zero only on top, not a problem \(f(x) = 0\)

3. if there is a zero on botton, the 2-sided limit will be \(\infty\text{,}\) \(- \infty\text{,}\) or DNE (will need more work)

4. if there are zeros on top and bottom is an indeterminate form (factor, simplify, rationalize, and take calc II)

   Note 1.2.10.

   Getting a result of \(\frac{0}{0}\) means the numberof the limit we are looking at gives \(p(a) = 0\) and \(q(a) = 0\) and that \(x-a\) is a factor of each polynomial; this factor can be divided out.