Skip to main content

Section 6.1 Exponential and Logrithmic Functions

A quick review of exponential and logrithmic functions.

Subsection 6.1.1 Exponential Functions

Note 6.1.1. The nine fules for exponents:.

  • \(\displaystyle a^m \cdot a^n = a^{m+n}\)

  • \(\displaystyle \left(a^m\right)^n = a^{m \cdot n}\)

  • \(\displaystyle \dfrac{a^m}{a^n} = a^{m-n} \)

  • \(\displaystyle a^0 = 1\)

  • \(\displaystyle a^{-1} = \dfrac{1}{a^n} \)

  • \(\displaystyle (a\cdot b)^n = a^n \cdot b^n \)

  • \(\displaystyle \left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}\)

  • \(\displaystyle a^{\frac{1}{n}} = \sqrt{a} \)

  • \(\displaystyle a^{\frac{m}{n}} = \left(\sqrt[n]{a}\right)^m \text{or } \sqrt[n]{(a)^m} \)

Definition 6.1.2. Exponential Function.

A function that can be written in the form \(f(x)=b^x\) where \(b > 0 \) and \(b \ne 1\) is called an exponential function.

Table 6.1.3. \(f(x)=2^x\)
x f(x)
-3 \(\frac{1}{8}\) \((2^{-3}=\frac{1}{8})\)
-2 \(\frac{1}{4}\) \((2^{-2}=\frac{1}{4})\)
-1 \(\frac{1}{2}\) \((2^{-1}=\frac{1}{2})\)
0 1 \((2^0 = 1)\)
1 2 \((2^1=2)\)
2 4 \((2^2=4)\)
3 8 \((2^3=8)\)

Figure 6.1.4.

Euler's Number.
\begin{equation*} e = \displaystyle \lim\limits_{n \to \pm \infty}\left(1+\frac{1}{n}\right)^n \approx 2.71828 \end{equation*}

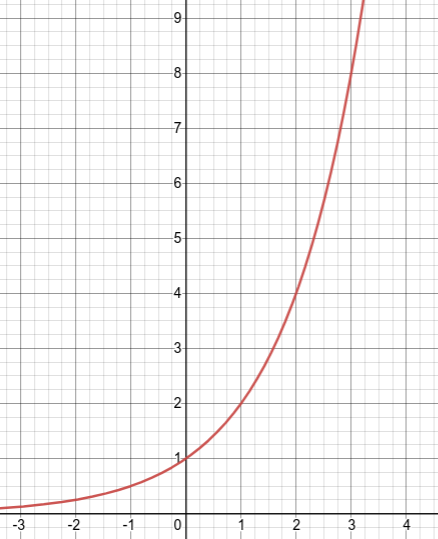
If you graph \(f(x)=\left(1+\frac{1}{x}\right)^x\text{,}\) you get a horizontal asymptote at \(y=e\text{.}\) If you graph \(y=e^x\) the slope of the tangent line at any point is equal to the height of the fundtion, therefore the derivative with respect to x of \(e^x\) is \(e^x\text{.}\)

Subsection 6.1.2 Logrithms

Note 6.1.5. The Five Properties of Algorithms.

  • \(\displaystyle log_a(a^m)= m \)

  • \(\displaystyle a^{log_a m} = m \)

  • \(\displaystyle log_a (m \cdot n) = log_a m + log_a n \)

  • \(\displaystyle log_a\left(\dfrac{m}{n}\right) = log_a m - log_a n \)

  • \(\displaystyle log_a (m ^ r) = r \cdot log_a m \)

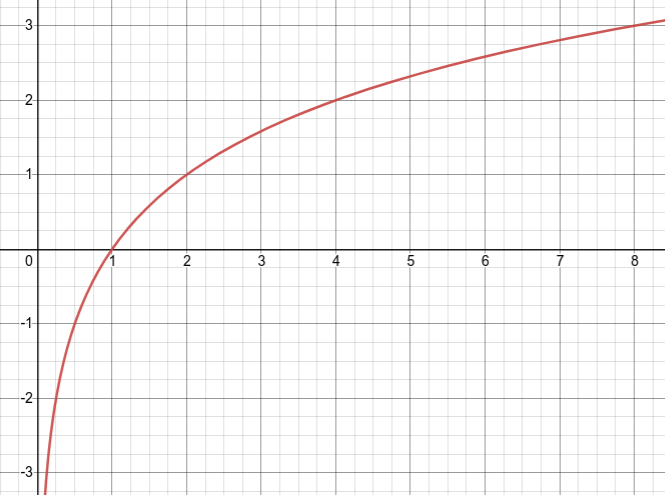
Definition 6.1.6. Logrithm.

If \(a > 0\) and \(a \neq 1\text{,}\) and if \(c > 0\text{,}\) then \(log_a c = b\) means \(a^b = c\text{.}\)

Table 6.1.7. \(f(x)=log_2 x\)
x f(x)
\(\frac{1}{8}\) -3 \((log_2 \frac{1}{8} = -3)\)
\(\frac{1}{4}\) -2 \((log_2 \frac{1}{4} = -2)\)
\(\frac{1}{2}\) -1 \((log_2 \frac{1}{2} = -1)\)
1 0 \((log_2 1 = 0)\)
2 1 \((log_2 2 = 1)\)
4 2 \((log_2 4 = 2)\)
8 3 \((log_a 8 = 2)\)

Figure 6.1.8.

Note 6.1.9. Additional Notation.

  • \(ln \rightarrow log_e \) "natural log"

  • \(log \rightarrow log_{10} \) "common log"

Change of Base Formula.

For any bases a and b (positive and \(\neq 1\)) and number M:

\begin{equation*} log_b M = \dfrac{log_a M}{log_a b} \end{equation*}