Skip to main content

Section 3.4 Applied Max-Min Problems

The goal of applying min/max principles to problems is to translate a word problem to a function and constraints.

There are a few general steps:

  1. draw a diagram and label

  2. find a formula to maximize or minimize

  3. reduce formula to a one-variable function

  4. find the interval based on physical constraints in the problem

  5. do your calculations

Example 3.4.1.

Given one fixed wall of any length necessary, maximize the area of the rectangular concept space. We have 10,000 feet of fencting.

  1. Draw:

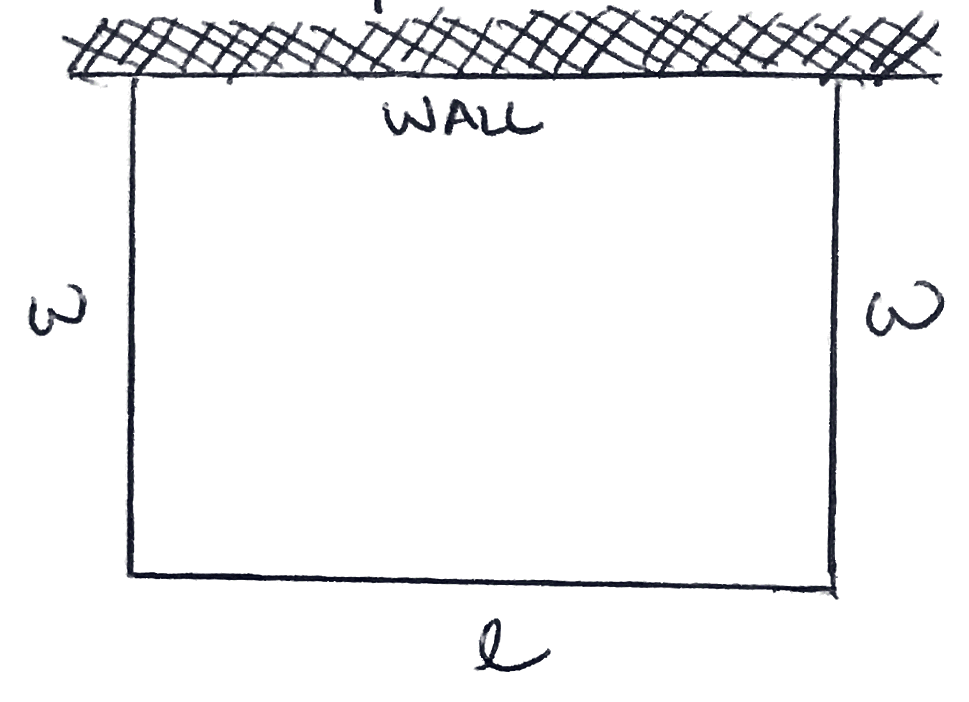
    Figure 3.4.1.

  2. Find a formula:

    \begin{equation*} A = w \cdot l \end{equation*}

  3. Reduce the formula to one variable:

    \begin{align*} 10000 \amp = 2w + l\\ 10000 - 2w \amp = l\\ \amp \Downarrow \\ A = f(w) \amp = w \cdot (10000 - 2w) \\ \amp = 10000w - 2w^2 \end{align*}

  4. Constraints and interval:

    Figure 3.4.2.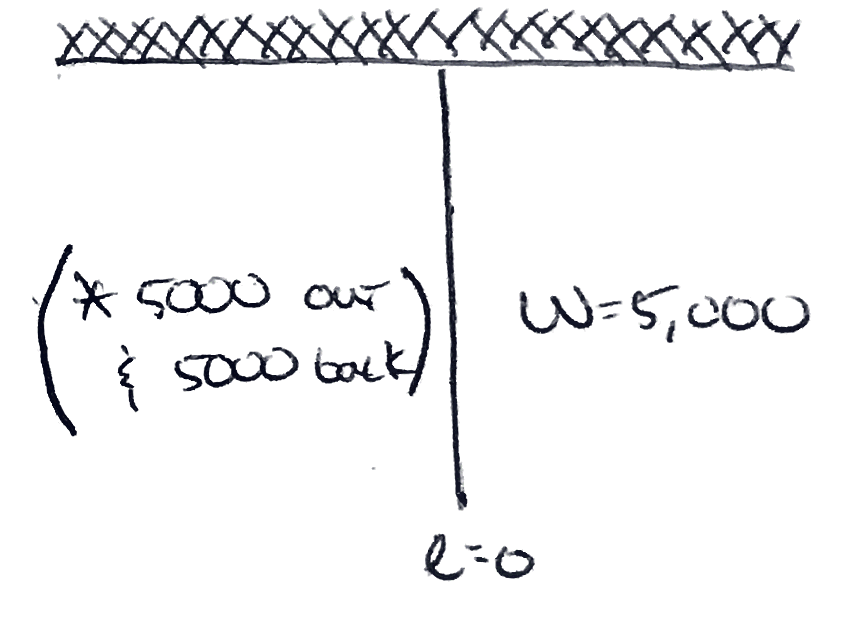

    Figure 3.4.3.

    If we just run it along the wall, we get the above.

    If we run the fence perpendicular to the wall and back, we get the above.

    So, \(0 \leq w \leq 5000\)

  5. Calculation:

    \begin{align*} \dfrac{dA}{dw} \amp = \dfrac{d}{dw}(10000w - 2w^2)\\ \amp = 10000 -4w \end{align*}

    critical points: \(10000 - 4w = 0 \Rightarrow\) w = 2500

    \(w\) \(A(w)\) Result
    (EP) \(0\) \(0\) ---
    (CP) \(2500\) \(12,500,000\) absolute max on \([0, 5000]\)
    (EP) \(0\) \(0\) ---

Conclusion:

  • The maximum area is \(12,500,000 ft^2\) with \(l=5000, w =2500\text{.}\)