Skip to main content

Section 1.1 Intro to Limits

Consisder the graph below, what is \(f(a)\text{?}\)

Figure 1.1.1.

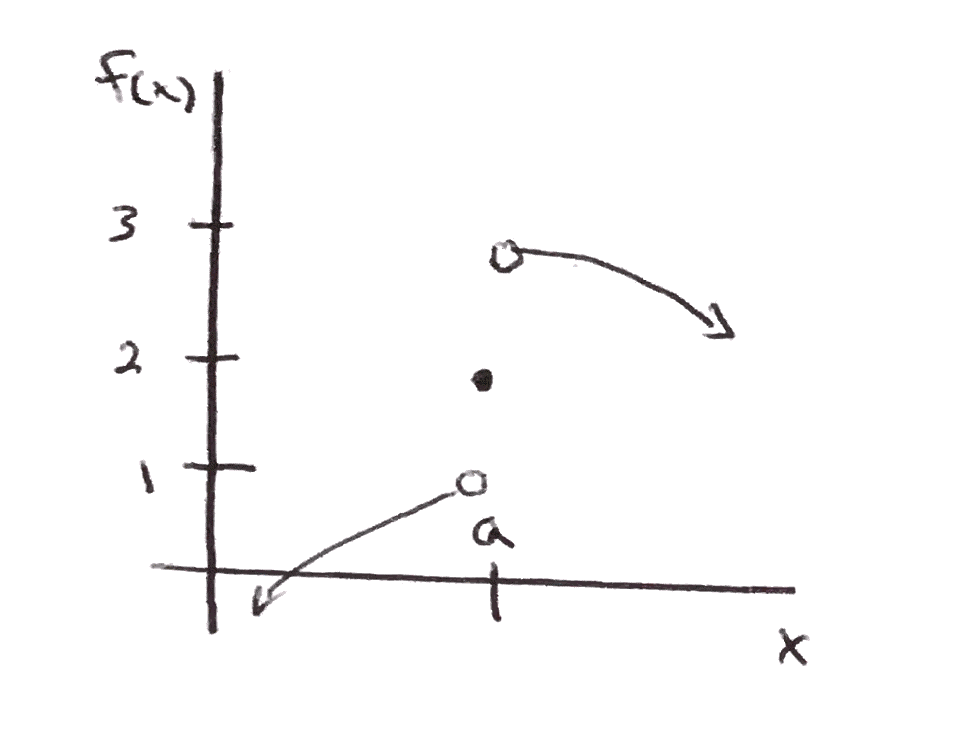
  • What is \(f(a)\text{?}\) \(f(a) = 2\)

  • Limits help answer the question, "what's going on near \(x=2\text{?}\)"

  • Answer: \(\displaystyle\lim_{x \to a} f(x) = \text{DNE (or Does Not Exist)}\text{.}\) The left and right side don't meet up at x = a.

We should look one side at a time using one sided limits:

  • from the left \(\displaystyle\lim_{x \to a^{-}} f(x) = 1\)

  • from the right \(\displaystyle\lim_{x \to a^{+}} f(x) = 3\)

Note 1.1.2.
Function values approach 1 as x approaches \(x = a\) from below

The pieces \(x \to a^{-} \text{ and } x \to a^{+}\) tell us about the direction we are approaching a number from.

Consider \(f(x) = 4 - x\text{:}\)

Figure 1.1.3.

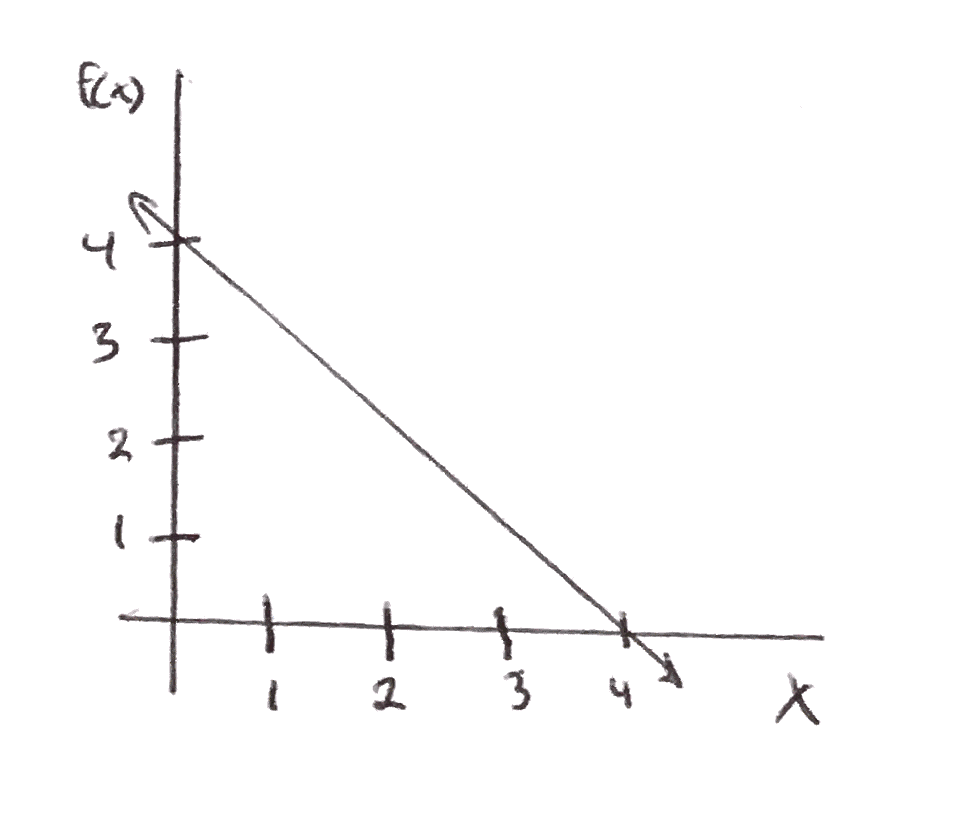
  • no strange features, just a straight line

  • \(\displaystyle \displaystyle\lim_{x \to 2^{-}} f(x) = 2\)

  • \(\displaystyle \displaystyle\lim_{x \to 2^{+}} f(x) = 2\)

Since the one-sided limts match, we get the two-sided limit:

\begin{equation*} \lim_{x \to 2} f(x) = 2 \end{equation*}

The function values of f(x) approaches 2 (from y-axis) as the input values approach 2 (from x-axis).

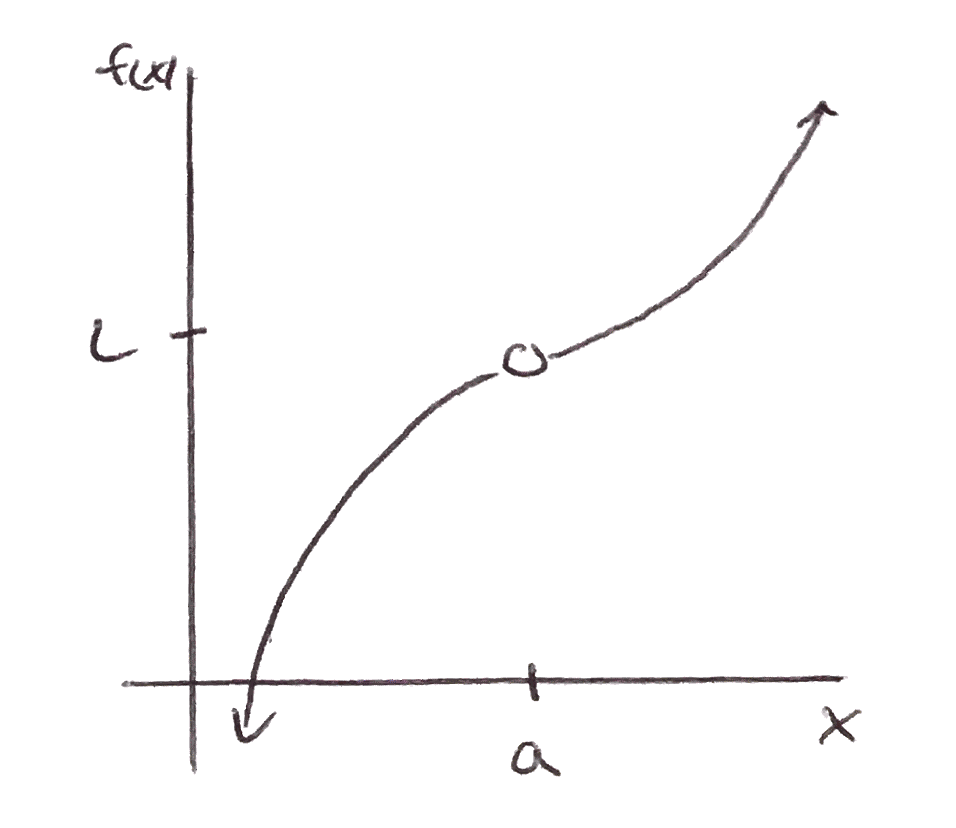
Consider the graph below:

Figure 1.1.4.

  • does this past the vertical line test? YES!

  • near \(x = 2\) the graph is a curve, at \(x = 2\) the value is zero

A limit can be used to help us describe this picture:

\begin{equation*} \displaystyle\lim_{x \to 2} f(x) = 2 \end{equation*}

This is read as "the limit of \(f(x)\) as x approaches 2 is 2".

Definition 1.1.5. Informal Definition of Limits.

Figure 1.1.6.

If the values of \(f(x)\) can be make arbitrarily close to \(L\) by taking values of \(x\) sufficiently close to, but not equal to some number \(a\text{,}\) then we write:

\begin{equation*} \lim_{x \to a} f(x) = L \end{equation*}

to mean either, "the limit of \(f(x)\) as \(x\) approaches \(a\) is \(L\)", or, "\(f(x)\) approaches \(L\) as \(x\) approaches \(a\)".

Consider \(f(x) = \dfrac{1}{x}\text{:}\)

Figure 1.1.7.

  • consider limits as we approach \(x=0\)

  • \(\displaystyle \displaystyle\lim_{x \to 0^{-}} f(x) = - \infty\)

  • \(\displaystyle \displaystyle\lim_{x \to 0^{+}} f(x) = \infty\)

  • each side is increasing without bound

Infinity is not a number, but exceeding all imaginable numbers in size. Since the limits differ, we say

\begin{equation*} \lim_{x \to 0} f(x) = DNE \end{equation*}

(both sides simultaneously, no superscript).

Function values go to different places as we approach from different sides of the number 0. The values of the limit is "DNE" since the graph does not meet up.

Subsection 1.1.1 Limits by Table

While this should generally be avoided, it can give us meaningful insights. Consider the function \(f(x) = \dfrac{1}{(x-5)^2}\text{.}\) Notice that \(f(5)\) is undefined as a result of an attempt to divide by zero.

Table 1.1.8.
\(\)x \(\dfrac{1}{(x-5)^2}\)
\(4\) \(1\)
\(4.9\) \(100\)
\(4.99\) \(10,000\)
\(5\) \(- \)
\(5.01\) \(10,000\)
\(5.1\) \(100\)
\(6\) \(1\)

  • \(\displaystyle \displaystyle\lim_{x \to 5^{-}} \dfrac{1}{(x-5)^2} = \infty\)

  • \(\displaystyle \displaystyle\lim_{x \to 5^{+}} \dfrac{1}{(x-5)^2} = \infty\)

  • unlike before we can actually state the two-sided limit: \(\displaystyle\lim_{x \to 5} \dfrac{1}{(x-5)^2} = \infty\)

We can make a sketch of the graph:
Figure 1.1.9.
Note 1.1.10.

Technicality: \(\infty\) is not a number, but we can't use it for arithmetic purposes. Technically the limit \(\displaystyle\lim_{x \to 0} \dfrac{1}{x} = DNE\) because the function does not approach a single number. Here the labeling as \(\infty\) provides useful info about the graph.

HINT: for a one-sided limit, we always use a number, \(\infty\text{,}\) \(- \infty\text{.}\) Reserve "DNE" for two-sided limits.